Formula of Spies vs Formula of Glynn

Introduction

Doing research for my book: A Bit of Math, The Art of Problem Solving, I stumbled on a Wikipedia article: Computing the permanent.

I Found the Balasubramanian–Bax–Franklin–Glynn formula. But wait a minute. Isn't this my very own formula from 2003? Looks almost the same! It is essentially the same!

In the end of 2002, early 2003 I solved Problem 29 of the NAW (see my Math Page). The solution was in terms of the permanent of a square (0,1)-matrix. For practical calculations I needed a fast algorithm. An implementation of Ryser's algorithm was one of the possibilities, but I found a formula at least as fast. The derivation was simple, almost elementary.

I implemented my alternative in a C/C++program, which was used to contribute to Neil Sloane's On-line Encyclopedia of Integer Sequences (OEIS). See for instance A087982, A088672 and A089476. Some of the records still stand! Maybe I should give it a try with the knowledge and computer power of today.

A short history from e-mails

Mails from and to Robbert Fokkink, Bruno Codenotti, Richard Brualdi, The American Mathematical Monthly, Neil Sloane and Edwin Clarke.

A compilation of the messages in text format: here.

In my e-mail of February 11th, 2003 I showed my results to Robbert Fokkink at that time the editor of the Problem Section of the NAW. As a conjecture. Robbert confirmed the correctness with a sketch of a proof. In the mean time I had written a short note with proof. How 'new' was the formula? Robbert made the suggestion to send an e-mail to an expert.

My message to Bruno Codenotti was answered with the suggestion to go straight to the master of permanents: Richard Brualdi. I owned a copy of his book: Brualdi, Ryser, Combinatorial Matrix Theory. This book has a chapter on permanents and was the source of my solution of problem 29. Brualdi and Ryser changed my life.

Richard Brualdi wrote: 'Your formula is interesting and I cannot recall seeing it before, but maybe it appears buried in some paper or other.' In a following message he suggested to send the result as a note to the American Mathematical Monthly.

With this recommendation I sent my note to the AMM on October 7th, 2003. In answer came an e-mail with the notification that my note was forwarded to Professor William Adkins for refereeing. The refereeing process could take several month and I would get an answer from Dr. Adkins from Louisiana State University. No such thing! After more than a year I asked: "What happened to my note? Was it to lightweighted and is it blown with the wind or what? I do have a version in a more substantial classic definition/theorem style." Additionally I mentioned the implementation of my algorithm in C++, faster than an optimized Ryser's code.

From October 2003 I put my program to work for the calculation of sequences related to permanents. See some discussions on this theme with Neil Sloane and Edwin Clarke. From Edwin Clarke: "Thanks for the copy of you note on permanents. It is an interesting approach. It might be a good idea to write it up as a new algorithm and compare it to known algorithms. It looks like the time is about 2^n which is certainly better than brute force n!."

In the years that followed I wrote a few things up in an article for the Nieuw Archief voor Wiskunde 5/7 nr. 4 December, 2006: Dancing School problems, Permanent solutions of Problem 29. A preprint can be found here. The article in print here. In a sidenote there is my formula for the permanent of a square matrix. See also the sidenote on The Van der Waerden Conjecture!

More recent developments

As I told in the Introduction I found this formula of Glynn. I was flabbergasted (I like that word!). Wrote an e-mail to my lifeline in Mathematics Robbert Fokkink. Robbert suggested to contact David Glynn in Adelaide. And yes, David replied after reading my long message.

A compilation of the messages in text format: here.

I quote: "It looks like you could be added to an increasing list of people that have rediscovered this formula for the permanent. (But the first I think was Balasubramanian in his PhD thesis in India.) My 2013 paper indeed shows that there are very many different formulae that are related via an algebraic structure called the Veronesean. Maybe I can get someone to put a reference to your articles around 2003-2006 or others on the wikipedia website so that it can be noted there. If you have trouble obtaining my reprints you could look at the researchgate site below where many of my papers can be downloaded."

Once again someone suggested me to write a short note for the American Mathematical Monthly. Again I did. If I may say so, it was a very readable manuscript. With emphasis on the elementary approach. With some history of the permanent. Just in an educational vein. This time the rejection was almost immediate.

The motivation: “In 2010, Glynn published ‘The permanent of a square matrix,’ a five-page note in The European Journal of Combinatorics that offered four different formulas for the matrix permanent. Now comes this manuscript, which offers an elementary proof of the first of these. The Monthly does publish new, elementary, proofs of old results, but only if the old results are famous, and/or the new proofs are beautiful and insightful. Unfortunately, neither of these applies here; on the contrary, Glynn’s proof was more insightful. Consequently, we must decline your submission for publication.”

I wrote to David Glynn: "So you win 4-1! And your proof was more 'insightful'. But imagine you have a class first year students, teaching some graph theory and you come to the permanent. Which method would you prefer giving some insight in the calculation of a permanent?" Do you prefer the insightful: "connected with invariant theory via the polarization identity for a symmetric tensor"?

The first e-mail from David Glynn was also his last one. All my messages ended in a black hole.

What next?

My programming skills are a little bit rusty, but I came up with an implementation of both the formula of Glynn and that of myself in Sage. SAGE, now SageMath, was started in 2005 by William Stein. I found SAGE at the end of 2005 and became an early adapter. In 2006 and later I contributed quite some code and more. Sage is Python+, so easy to learn and use. SageMath tries to be an Open Source alternative for the big M's: Magma, Mathematica, Maple and Matlab. And integrates a lot of other Math software. SageMath is a free open-source mathematics software system.

SageMath has various options to calculate the permanent of matrices over a field. Guess who implemented Ryser's algorithm? In the demo worksheet we calculate the permanent of the example in Glynn's 2010 article. Look for the differences: In Glynn's formula you see row sums in the iterations in mine col sums. This is due to the use of right or left multiplication in matrix theory. Results are the same, of course: the sum of all diagonal products!

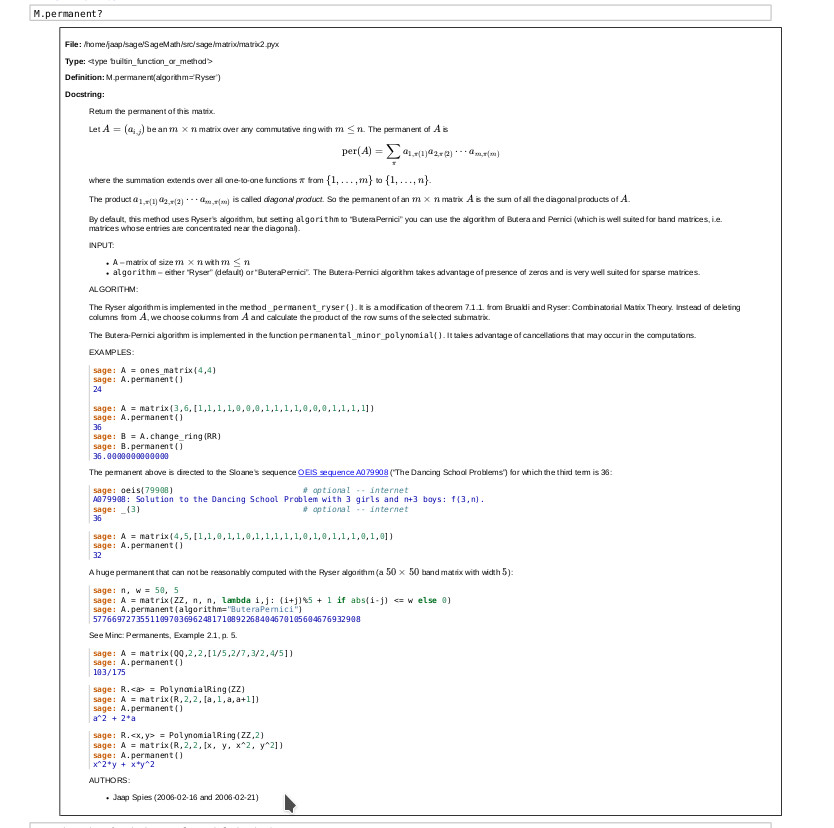I did some timings too, see here. The default implementation wins of course, because it is written in Cython. Cython is an optimising compiler for Python code.

Important note: The permanent fuction in SageMath accepts rectangular matrices! The formula of Spies (and that of Glynn) works only for square matrices.

And now?

In the NAW 5/21 nr. 1 March 2020 there is an article "A formula for the permanent".

In the Dutch Wikipedia page on Permanents we now see the formula of Spies.

I still hope there will be an addition to the English versio of the Wikipedia page! Volonteers!